Везде
Оптимальное решение задачи иммунизации потока множественных платежей произвольной структуры
Оглавление
Аннотация Оценить Содержание публикации
Библиография Комментарии
Поделиться
QR
Метрика
Оптимальное решение задачи иммунизации потока множественных платежей произвольной структуры
Аннотация
Код статьи
S042473880025861-6-1
DOI
10.31857/S042473880025861-6
Тип публикации
Статья
Статус публикации
Опубликовано
Авторы
Курочкин Сергей Владимирович 
Аффилиация: НИУ ВШЭ
Адрес: Москва, Россия
Родина Виктория Алексеевна
Аффилиация: НИУ ВШЭ
Адрес: Россия
Выпуск
Том 59 № 2
Страницы
87-99
Аннотация

sup-норма функции шока ставок — зависит только от изменения кривой бескупонной доходности. Доказана неулучшаемость оценки. Получен явный вид и алгоритм расчета оптимального иммунизирующего портфеля. Практическая применимость метода продемонстрирована на примере иммунизации портфеля облигаций федерального займа при структуре потока обязательств типа аннуитета.

Ключевые слова
ALM, иммунизация, процентный риск, мера разброса, метрика Монжа–Канторовича–Вассерштейна, EMD-расстояние.
Классификатор
Получено
02.06.2023
Дата публикации
02.07.2023
Всего подписок
12
Всего просмотров
216
Оценка читателей
0.0 (0 голосов)
Цитировать   Скачать pdf
1 1. Введение
2 В настоящее время интегрированное управление портфелями активов и обязательств (asset-liability management, ALM) относится к классу лучших международных практик. Прежде всего это касается пенсионных фондов и страховых компаний, но также затрагивает и других финансовых посредников, имеющих портфели средне- и долгосрочных обязательств, таких как коммерческие и инвестиционные банки, и управляющих частным капиталом. Стратегии и техники в ALM разнообразны (см., например, классификацию (Leibowitz, 1986; Van der Meer, Smink, 1993)) и нацелены на контроль спектра рисков, но главным среди них всегда остается процентный риск1.
1. Здесь и далее по тексту под процентным риском (interest rate risk) мы будем понимать отрицательный эффект от движения процентных ставок в любом направлении. При конкретизации направления движения понятие процентного риска сужается либо до ценового риска (price risk), либо до риска реинвестирования (reinvestment risk).
3 Неопределенность движения процентных ставок является главной сложностью при управлении портфелями, находящимися «по разные стороны баланса» и состоящими из чувствительных к движению процентных ставок инструментов, а асимметричность изменения их стоимостей после реализации процентного риска — крайне нежелательным следствием. Классическая теория иммунизации, выдвинутая Фрэнком Редингтоном в 1952 г., явилась первым ответом на эти вызовы.
4 Заметим, что классическую модель стали использовать на практике весьма оперативно в Великобритании, где была опубликована работа Фрэнка Редингтона (Vanderhoof, 1972). Вместе с тем осмысление того, что природа неопределенности движения процентных ставок очень далека от упрощенной схемы аддитивного шока форвардных ставок в классической модели, запустило процесс эволюции научных взглядов на то, какой должна быть правильная иммунизация, длящийся до сих пор. Были предложены многочисленные подходы к оценке и контролю процентного риска. Но только их часть и только для иммунизации единичного2 платежа подходит для практического применения. Остальные подходы скорее интеллектуально привлекательны для научного сообщества. Но если для обязательств с единичным платежом утверждение, что иммунизация является мощным инструментом обращения с процентным риском в портфельном управлении, все-таки справедливо, то для случая множественных платежей утверждение остается только в области абстракции.
2. В контексте настоящей работы прилагательное «единичный» понимается как однократный.
5 А между тем множественные выплаты генерируют и портфели пенсионных планов, и портфели страховых полисов (когда в страховые полисы заложены аннуитетные компенсации). Для таких портфелей, в отличие от портфелей обязательств с единичной выплатой, и по сей день не существует иммунизирующих механизмов. Потребность в них диктуется жесткими регуляторными ограничениями для пенсионных фондов и страховых компаний в отношении финансовой устойчивости их бизнес-модели.
6 Поскольку модели иммунизации денежного потока с единичной выплатой не работают для потока множественных выплат, хеджирование, как правило, осуществляется на базе решения задачи линейного программирования в рамках альтернативной для иммунизации концепции балансировки по платежам (cash flow matching). Модели балансировки по платежам также относятся к ALM и примечательно, что они применялись до появления классической иммунизации.
7 Новое развитие модели балансировки по платежам получили в 1990-е годы в работах (Rosenbloom, Shiu, 1990; Ford, 1991, 1993). Однако эти модели все же являются инструментом ad hoc. Не будучи порождением финансовой науки, они не имеют достаточного теоретического фундамента, уязвимы в отношении обосновывающих критериев, а решением задачи линейного программирования может стать неестественный и неэффективный портфель. Как статичная модель, предполагающая изначальное равенство двух денежных потоков, балансировка по платежам обходится дорого и может не иметь решения без большого числа коротких позиций. Как динамическая модель, ситуативно выравнивающая два денежных потока, она уязвима ввиду ошибочных прогнозов будущих ставок по займам и депозитам, а фактическая реализация стратегии в части заимствования денежных средств может приводить к нарушению внутренних установок по нормам ликвидности. Задачей же ALM для пенсионных фондов и страховых компаний является формирование стратегического портфеля, обеспечивающего бесперебойное функционирование. Этого можно добиться дальнейшим прогрессом в моделировании иммунизации.
8 В настоящей работе предложена модель иммунизации потока множественных платежей с минимизацией меры разброса, опирающаяся на теоретические результаты в (Fong, Vasicek, 1984; Nawalkha, Chambers, 1996; Balbas, Ibanez, 1998). В этих работах был предложен и формализован подход, в рамках которого остаточный процентный риск, неустранимый посредством наложения ограничений дюрацией Фишера–Вейла, оценивается количественно и подлежит минимизации. В свое время понимание того, что дюрация Фишера–Вейла неэффективна при непараллельных сдвигах спотовой кривой, породило многочисленные попытки получить улучшенные метрики, при применении которых действенность иммунизирующего механизма не могла бы быть существенно скомпрометирована ошибочными прогнозами движения процентных ставок.
9 В моделях иммунизации с мерой разброса в (Fong, Vasicek, 1984; Balbas, Ibanez, 1998) предлагается оставить за дюрацией Фишера–Вейла хеджирующую от параллельных сдвигов спотовой кривой функцию и сосредоточиться на проблеме минимизации остаточного процентного риска, а в (Nawalkha, Chambers, 1996) — полностью свести задачу иммунизации к минимизации остаточного процентного риска. Последнее объясняется тем, что в вышеперечисленных работах, в отличие от работ в рамках других подходов к моделированию правильной иммунизации, допущения о шоке форвардных ставок минимально рестриктивные, что существенно усиливает иммунизирующий потенциал модели и делает соблюдение дюрации Фишера–Вейла излишним условием.
10 В (Fong, Vasicek, 1984; Nawalkha, Chambers, 1996; Balbas, Ibanez, 1998) выводится неравенство, в котором один компонент показывает максимально допустимое возмущение спотовой кривой, а второй — чувствительность портфеля, генерирующего единичную выплату, к такому возмущению, называемую мерой разброса. Формальное представление меры разброса — важный шаг в моделировании иммунизации. Мы развиваем теоретический результат (Nawalkha, Chambers, 1996) и предлагаем модель иммунизации с мерой разброса, подходящую для хеджирования потока как с единичным, так и с множественными платежами при сохранении минимально рестриктивных допущений о шоке форвардных ставок. Главная трудность метода состоит в том, что мера разброса M-Absolute, полученная в (Nawalkha, Chambers, 1996), не может быть обобщена напрямую. Для такого обобщения требуется другая конструкция. Подходящей конструкцией является метрика Монжа–Канторовича–Вассерштейна. Данное понятие было введено Гаспаром Монжем еще в 1781 г. (Monge, 1781), а затем многократно, под различными названиями и с различными вариациями, открывалось заново, изучалось и применялось в теории меры, теории транспортных задач, методах распознавания образов и т.д.3 Метрика Монжа–Канторовича–Вассерштейна — количественная мера близости многомерных объектов (изображений, гистограмм, персистентных диаграмм и т.п.) — широко и результативно применяется в современных приложениях искусственного интеллекта и методах машинного обучения (Panaretos, Zemel, 2019; Torres et al., 2021). В настоящей работе для ее обозначения будет использован краткий термин «EMD-расстояние» (earth mover’s distance).
3. С историей вопроса можно ознакомиться в (Богачев, Колесников, 2012).
11 В настоящей работе впервые предложено решение проблемы иммунизации портфеля облигаций для случая множественных платежей по обязательствам и сдвигов кривой доходности произвольной структуры. Ключевым новым результатом работы является оценка типа Фонга–Васичека — величина процентного риска, т.е. отклонение в отрицательную сторону стоимости портфеля активов от приведенной стоимости потока обязательств, вызванное изменением ставок спот, ограничено произведением двух сомножителей, один из которых представляет EMD-расстояние между потоками активов и обязательств и зависит только от структуры портфеля, а другой — sup-норма функции шока ставок — зависит только от изменения кривой бескупонной доходности. Такая оценка неулучшаема в классе функций изменений ставок произвольной формы (без предположений гладкости). Для реализующего ее, т.е. оптимального, портфеля получена его структура и способ расчета.
12 Конструирование меры разброса и оптимального иммунизирующего портфеля для случая множественных платежей дополняется апробацией на реальных данных. Показано, что иммунизация с минимизацией EMD-расстояния является готовым руководством к действию для практиков. При этом, имея психологически-комфортный прескриптивный характер, предлагаемое нами решение выгодно отличается от хеджирования потока множественных платежей в моделях балансировки по платежам, поскольку совмещает необременительность прикладного применения со строгим теоретическим обоснованием.
13 Структура работы следующая. В разд. 2 описана логика возникновения моделей иммунизации с минимизацией меры разброса и представлены теоретические результаты данного направления. В разд. 3 получено основное неравенство для оценки процентного риска через меру близости потоков платежей по активам и обязательствам произвольной структуры. В разд. 4 показана неулучшаемость данной оценки, поставлена задача оптимальной иммунизации и приведен алгоритм ее решения. В разд. 5 проведена апробация конструкции на реальных данных. В заключении сформулированы выводы и открытые вопросы.
14 2. Обзор литературы: краткая история вопроса и теоретические результаты
15 Идея хеджирования потока выплат потоком поступлений по критерию срочности получила завершенное оформление в работе Фрэнка Редингтона (Redington, 1952). Он ввел термин «иммунизация» (immunization), с тех пор прочно закрепившийся в профессиональной лексике. В классической теории иммунизации Редингтона выдвигаются два необходимых и достаточных условия.
16 Условия Редингтона.
17
  1. Для портфелей активов и обязательств двух равенств одновременно соблюдаются их настоящие стоимости и их дюрации4.
  2. Разброс взвешенных сроков по поступлениям должен превышать таковой по выплатам.
4. Фрэнк Редингтон не использовал термина «дюрация» (duration), введенного Фредериком Маколеем, о работе которого он просто не знал. В современном изложении с использованием термина «дюрация» теория иммунизации впервые появилась в работах (Fisher, Weil, 1971; Vanderhoof, 1972; Weil, 1973).
18 Допущения, принятые в классической теории иммунизации. В классической теории формулируется ряд допущений, при этом основной траекторией дальнейшего развития теории стало ослабление следующих допущений:
19
  1. спотовая кривая является плоской,
  2. возмущение спотовой кривой описывается параллельным сдвигом,
  3. возмущение спотовой кривой незначительное.
20 Заметим, что в классической теории допускаются множественные платежи по обязательствам, однако в полной мере предметно развить данное направление не удалось.
21 В ранних работах, в которых впервые ослабляются первое и второе допущения (Fisher, Weil, 1971; Bierwag, Khang, 1977; Khang, 1979), изменения форвардных ставок описываются шоком аддитивного, мультипликативного и затухающего по срочности воздействия посредством введения соответствующих констант. Как следствие — изменения форвардных ставок функционально зависимы и абсолютно коррелированы. Уже в (Ingersoll, Skelton, Weil, 1978) было продемонстрировано, что подобные установки моделирования неопределенности движения процентных ставок приводят к логическому парадоксу. Это связано с тем, что сформированные в подобных установках иммунизированные портфели несовместимы с принципом отсутствия арбитражных возможностей и их существование в условиях общего рыночного равновесия неминуемо означает движение процентных ставок, отличное от первоначально прогнозируемого. После этого теория иммунизации получила новое осмысление и с 1980-х годов демонстрирует разветвленность, характеризуемую тем, какое именно обращение с базовыми установками лежит в основе изменений.
22 Моделирование иммунизации с минимизацией меры разброса является ключевой в контексте настоящей работы ветвью развития теории иммунизации. В общих чертах, это — поддержание (а потом отталкивание от) зонтичной идеи о том, что при невозможности совершенно корректной идентификации качества и числа диффузионных процессов в моделировании неопределенности движения процентных ставок лучшим выходом будет принять неизбежность остаточного процентного риска5 (появляющегося после устранения процентного риска посредством балансировки по дюрациям), его формализовать и минимизировать. Для того чтобы задача оптимизации дала независимое решение, работающее при разнообразных возмущениях спотовой кривой, в моделировании неопределенности устанавливаются минимальные допущения.
5. По-английски данный риск именуется stochastic process risk (либо просто process risk), или immunization risk.
23 Впервые такой иммунизирующий механизм представлен в (Fong, Vasicek, 1984). Авторы показали, что падение конечной стоимости портфеля активов вследствие изменения процентных ставок имеет нижнюю границу, существование которой не обусловлено типом возмущения спотовой кривой. Для аддитивного шока форвардных ставок Δit теорема Фонга–Васичека утверждает:
24 ΔVH/VH≥-0,5KM2,  (1)
25 M2=1V0∑k=1natktk-H2,  (2)
26 где V0 , VH — стоимости портфеля активов в момент времени 0 и H соответственно; tk  — момент времени денежного поступления в портфель ( k=1,  ...,  n ); atk  — настоящая стоимость денежного поступления At в портфель; K  — верхняя граница изменения наклона по всей временной структуре вплоть до срока T . Неравенство (1) показывает, что неблагоприятное изменение конечной стоимости портфеля активов ограничено снизу произведением двух величин, первая из которых, -0,5K , зависит только от шока форвардных ставок, вторая M2  — только от структуры активов.
27 Поскольку в (1) только структура активов является подконтрольным свойством, она будет переменной выбора в задаче минимизации последствий несовершенной иммунизации посредством балансировки по дюрациям, которые количественно выражены целевой функцией M2 , с наложением ограничений по первому допущению Редингтона. В соответствии с (2), M2  — взвешенное среднее квадратов расстояний между моментами времени денежных поступлений и горизонтом инвестирования. Примерная структура активов, соответствующая решению задачи минимизации, — так называемый залповый портфель (bullet portfolio).
28 В работах (Shiu, 1987, 1990) обобщены результаты (Fong, Vasicek, 1984) и уточнены ограничения, при которых результат (Fong, Vasicek, 1984) справедлив. В (Montrucchio, Peccati, 1991) общие выводы (Shiu, 1987) обобщаются далее, включая случай, когда функция, описывающая шок форвардных ставок, может быть недифференцируемой и скачкообразной. Также дано уточнение для основного неравенства в (Fong, Vasicek, 1984). В (Bierwag, Fooladi, Roberts, 1993) показано, что M2 эффективно минимизирует остаточный процентный риск только для узкого класса стохастических процессов, а портфель с минимальным значением M2 против ожиданий не всегда будет залповым.
29 В (Nawalkha, Chambers, 1997; Nawalkha, Soto, Zhang, 2003) авторы развивают меру M2 до Q-компонентной структуры — M-вектора — через разложение изменения прироста одной денежной единицы в ряд Тейлора порядка Q+1 . При Q=2 M-вектор сводится к M2 . Если Q>2 , то, по утверждению (Nawalkha, Chambers, 1997), можно добиться почти совершенной иммунизации, так как увеличение элементов в M-векторе позволяет лучше учитывать отдаленность моментов времени денежных поступлений от горизонта инвестирования H и позволяет отразить более тонкие нюансы возмущения спотовой кривой.
30 Мера M2 является квадратичной мерой разброса денежных поступлений относительно горизонта инвестирования. В (Balbas, Ibanez, 1998; Balbas, Ibanez, Lopez, 2002) была введена схожая мера линейного разброса. Так же, как и в (Fong, Vasicek, 1984), у авторов вводится параметр, определяющий наихудший (в рамках разумных и реалистичных предположений) сценарий изменения спотовой кривой.
31 В моделях (Fong, Vasicek, 1984; Shiu, 1987, 1990; Balbas, Ibanez, 1998), равно как и в их обобщениях, соблюдается правило: среди всех портфелей, выполняющих первое условие Редингтона, выбирается один с наименьшим значением меры разброса. Также имеется схожая характеристика: аддитивность шока форвардных ставок с допущением произвольной структуры по срочности. Поэтому такие модели иммунизируют:
32
  • как в случае незначительных, так и в случае значительных возмущений спотовой кривой и ослабляют допущение;
  • от разнообразия проявлений процентного риска, например от скручивания и раскручивания (twist) спотовой кривой.
33 Наконец, в (Nawalkha, Chambers, 1996) выдвигается модель иммунизации, которая сохраняет вышеперечисленные преимущества, но отличается более гибкой постановкой задачи оптимизации. В модели снимается ограничение на точное соблюдение первого условия Редингтона и подбирается мера разброса, которая возьмет на себя функцию минимизации не остаточного, а совокупного процентного риска. Если кроме предположения, что шок форвардных ставок является ограниченной функцией, не делается других предпосылок относительно возмущения спотовой кривой, то нет необходимости в жестком разграничении иммунизирующих функций между дюрацией, использование которой направлено на устранение неблагоприятных последствий параллельных сдвигов, и мерой разброса, минимизация которой устраняет остаточный процентный риск. Поддержка этой идеи исходит, в том числе, и из того что в условиях неполноты рынка портфель с требуемой дюрацией можно и не сформировать. Основное неравенство в (Nawalkha, Chambers, 1996) имеет вид:
34 ΔVH/VH≥-K3MA,  (3)
35 Где
36 MA=1V0∑k=1natktk-H,  (4)
37 K3=maxK1,K2,    K1≤Δit≤K2    ∀t≥0. (5)
38 Мера разброса M-Absolute ( MA ) представлена в (4); это — взвешенное среднее абсолютное расстояние между моментом времени поступления денег и горизонтом инвестирования. Мера, характеризующая возмущение спотовой кривой, дана в (5). Это максимальное отклонение форвардной кривой в большую или меньшую сторону. Как и прежде, минимизации подлежит компонент, который можно контролировать дизайном портфеля активов. Авторы (Nawalkha, Chambers, 1996) заявляют, что только в гипотетическом случае незначительного параллельного сдвига спотовой кривой иммунизация по дюрации Фишера–Вейла сработает лучше. Во всех реалистичных случаях иммунизация мерой M-Absolute окажется эффективнее.
39 На случай множественных платежей меры разброса распространены не были, если не считать условный пример в (Fabozzi, Fong, 1985), где с весьма ограничивающим предположением, что шок форвардных ставок является линейной функцией от срочности, получено приближенное выражение для изменения стоимости портфеля, содержащее неточности.
40 В теории иммунизации известно несколько работ, в которых прорабатывается вопрос множественных платежей. В (Bierwag, Kaufman, Toevs, 1983) дано решение как для совместимых, так и для несовместимых с общим экономическим равновесием предпосылок относительно возмущения спотовой кривой. В первом случае первое условие Редингтона является необходимым и достаточным, во втором случае — только необходимым, а достаточность достигается выполнением второго условия Редингтона в таком виде, что формируются два портфеля активов, для которых сроки первой и последней выплаты по портфелю обязательств будут верхней и нижней границей дюрации соответственно. В (Shiu, 1988) проблема рассматривается для общего случая: если возмущения спотовой кривой описываются выпуклой функцией, то разбивка на портфели активов выполняется так, чтобы каждая выплата по портфелю обязательств была иммунизирована отдельно, — что является необходимым и достаточным условием. Результаты (Shiu, 1988) были развиты и обобщены в (Shiu, 1990; Hürlimann, 2002). Отметим, что ни одна из вышеперечисленных работ не имеет прикладного характера и по-видимому даже приближенно не может рассматриваться как руководство к действию для практиков.
41 С точки зрения практического применения интересна работа (Theobald, Yallup, 2009), в которой предложена модель иммунизации на основе обобщения первого условия Редингтона на m+1 моментов иммунизации, где дюрация будет частным случаем при m=1 . Отметим, что здесь неизбежна проблема выбора (trade-off), не имеющая места в модели иммунизации, выдвинутой в настоящей работе: повышение точности посредством увеличения слагаемых высшего порядка в ряде Маклорена усложняет работу оптимизационного механизма. Похожий подход используется в (De La Peña, 2021; Бешенов, Лапшин, 2019).
42 С начала 1990-х годов, когда отставание в разработках иммунизирующих механизмов для множественных платежей в сравнении с таковыми для единовременного платежа становится особенно явным, появляются работы об управлении портфелями активов и обязательств с фокусом на технике балансировки по платежам (Rosenbloom, Shiu, 1990; Ford, 1991, 1993). К настоящему времени возникающая здесь задача оптимизации сильно усложнилась технически. В публикациях предлагается применение стохастического линейного (Dutta et al., 2019) и нелинейного (Kopa, Rusý, 2021) программирования с симуляциями Монте-Карло для оценки риска неплатежей (Bayliss et al., 2020). Однако, как разъяснено во введении, техника балансировки по платежам будет скорее вынужденной альтернативой и, ввиду слабой концептуальности и собственных погрешностей, не делает менее актуальными поиски полноценного иммунизирующего механизма на случай, когда по обязательствам совершаются множественные платежи.
43 3. Основное неравенство
44 Основное неравенство (см. формулу (12)) есть результат ослабления допущения о единичном платеже по обязательствам, которое, не будучи заявленным Редингтоном, тем не менее, стало неизменным условием моделирования иммунизации. В остальном мы ослабляем допущения 1)–3) так же, как это сделано в работах, в которых иммунизация моделируется с минимизацией меры разброса.
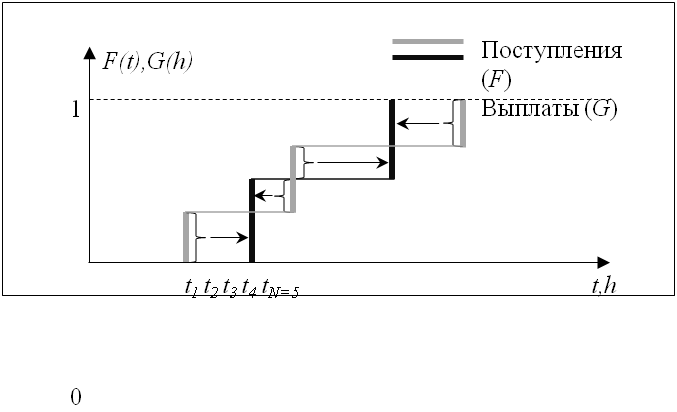
45 Пусть имеются потоки платежей по портфелю активов и обязательств — Atk и Ltk соответственно, где k=1,…,N  — моменты времени наступления платежей. Не нарушая общности, можно считать, что моменты времени синхронизированы, полагая недостающие платежи равными нулю. Короткие позиции не допускаются, т.е. Atk≥0 .
46 Введем необходимые обозначения. Пусть it и Δit — форвардная ставка на момент времени t по состоянию на настоящий момент и шок форвардной ставки соответственно; Wt=exp-∫0tiτdτ — дисконтная функция; VA,0 и VL,0  — настоящая стоимость портфелей активов и обязательств соответственно;
47 VA,0=∑t=t1tNAtW, (6)
48 VL,0=∑t=t1tNLtWt; (7)
49 ΔVA,0 и ΔVL,0 — изменение настоящей стоимости вследствие шока форвардной для портфелей активов и обязательств соответственно,
50 ΔVA,0=∑t=t1tNAtWtexp-∫0tΔiτdτ-1,     ΔVL,0=∑t=t1tNLtWtexp-∫0tΔiτdτ-1;
51 Δi  — величина шока форвардной ставки в норме равномерной сходимости, Δi=supΔiτ,    τ∈0,tN.
52 Считаем (как принято в таких случаях), что активы куплены на привлеченные средства, т.е. VA,0=VL,0 6. Исследуем расхождение в стоимости портфелей активов и обязательств, которое может произойти вследствие шока форвардной ставки. Предварительно рассмотрим ситуацию единичной выплаты по обязательствам LH , приходящейся на момент времени t=H. Тогда
6. В различных прикладных областях условия типа нормировки часто не соответствуют сути задачи, в связи с чем в ряде работ рассматриваются так называемые несбалансированные транспортные задачи и вводятся расстояния между мерами, не удовлетворяющие условиям нормированности и даже знакоопределенности (Chizat, 2018; Gangbo et al., 2019).
53 ΔVL,0=VL,0exp-∫0HΔiτdτ-1.
54 Учитывая равенство VA,0=VL,0 и (6), имеем
55 ΔVA,0-VL,0=VA,0+ΔVA,0-VL,0-ΔVL,0=∑t=t1tNAtWtexp∫0tΔiτdτ-exp∫0HΔiτdτ. (8)
56 Выражение в скобках в (8) можно представить как
57 exp-∫0tΔiτdτ-exp-∫0HΔiτdτ=exp-∫0HΔiτdτexp-∫HtΔiτdτ.  (9)
58 Для первого сомножителя в правой части (9) справедливо неравенство exp-∫0HΔiτdτ≤expHΔi. Здесь Δi  — по своему смыслу малая величина, так что все выражение имеет порядок единицы7 и может быть оценено как expHΔi≤1+ε , ε  — малая величина. Для второго сомножителя в (9), учитывая, что ex≥1+x , справедливо неравенство
7. Например, при горизонте H=20 лет и контролируемом изменении процентных ставок Δi=±25 базисных пунктов, eHΔi≈1,0513.
59 exp-∫HtΔiτdτ-1≥-∫HtΔiτdτ≥-H-t    Δi.
60 Переходя к относительным изменениям, окончательно получаем
61 ΔVA,0-VL,0/VL,0=∑t=t1tNAtWtexp-∫0HΔiτdτexp-∫HtΔiτdτ-1/VL,0,
62 ΔVA,0-VL,0/VL,0≥∑t=t1tNAtWt/VL,0-1+εH-t  Δi.  (10)
63 Поскольку, по определению, VA,0=∑t=t1tNAtWt , величины AtWt/VA,0 являются весами отдельных поступлений в денежном потоке по активам (как веса в стандартной формуле дюрации). Оценка (10) аналогична основному результату в (Nawalkha, Chambers, 1996), см. (1)–(3), с той лишь разницей, что там стоимости денежных потоков и их изменений вследствие шока форвардных ставок приводятся к моменту времени t=H , в то время как в (10) они приведены к моменту времени t=0 , поэтому возникает множитель 1+ε . Действовать именно так естественно, поскольку в настоящей работе у рассматриваемого произвольного потока выплат по обязательствам нет одного выделенного срока H . Кроме того, дисконтирование к настоящему моменту, а не к какому-либо моменту времени в будущем, соответствует общепринятой финансовой практике.
64 Обратимся к общему случаю произвольного потока выплат. Предположим, что для каждого платежа Lh из Lhh=t1,…,tN для портфеля обязательств указаны (пока каким-либо произвольным образом, но далее возникнет задача оптимизации) финансирующие его платежи Ath из Atht,h=t1,…,tN , представляющие собой части платежей At . В совокупности Ath образуют транспортный план. Тогда имеем:
65 ∑t=t1tNAthWt=LhWh,     ∑h=t1tNAth=At,     VA,0=∑h=t1tN∑t=t1tNAthWt=∑h=t1tNLhWh=VL,0.
66 Повторяя конструкцию для случая единичной выплаты LH в (10) и соответственно применяя (10) для каждого Lh , после суммирования имеем
67 ΔVA,0-VL,0=∑h=t1tNΔ∑t=t1tNAthWt-LhWh≥-1+ε∑h=t1tN∑t=t1tNAthWth-t  Δi. (11)
68 Таким образом, процентный риск в абсолютном выражении ограничен произведением двух (не считая множителя (1+ε) ) величин, из которых одна ( ∑h=t1tN∑t=t1tNAthWth-t ) зависит от денежных потоков по портфелям активов и обязательств и спотовой кривой, наблюдаемой сейчас, и не зависит от возможных возмущений спотовой кривой в будущем; вторая ( Δi ) представляет величину изменения форвардных ставок в смысле максимум-нормы в пространстве функций.
69 Далее, введем величины ath=AthWt/VA,0. Очевидно, что ath≥0,     t,  h=1,…,N и что ∑h∑tath=1 . Тогда величина γt=∑hath=∑hAthWt/VA,0=AtWt/VA,0  — вес (с учетом дисконтирования) платежа t в портфеле активов. Величина λh=∑tath=∑tathWt/VA,0=LhWh/VL,0 (учтено равенство VA,0=VL,0 ) — вес (с учетом дисконтирования) платежа h в портфеле обязательств.
70 Понимая ath как вероятностную меру, видим, что ее частные распределения совпадают с относительными распределениями платежей, соответственно, по активам и обязательствам, а каждое отдельное ath представляет собой, в дисконтированном и нормированном виде, часть платежа t по активам, направляемую на финансирование платежа h по обязательствам. Делим (11) на VA,0 и получаем основное неравенство
71 ΔVA,0-VL,0VA,0≥-1+ε∑h=t1tN∑t=t1tNAthWth-tVA,0Δi.  (12)
72 Выражение
73 ∑h=t1tN∑t=t1tNAthWth-tVA,0=∑h∑tathh-t
74 в правой части (12) в точности представляет собой функционал, фигурирующий в определении метрики Монжа–Канторовича–Вассерштейна, или EMD-расстояния. Расстояние EMD есть минимум такого функционала, взятый по всевозможным транспортным планам ath .
75 Данная мера близости потоков платежей по портфелям активов и обязательств в отличие от мер разброса, представленных в обзоре литературы, имеет прямой финансовый смысл. Стоимость перемещения одной денежной единицы (без учета временной стоимости) на один год варьирует от 50 до 100% величины банковского спреда в зависимости от типа участника долгового рынка. Тогда EMD-расстояние дает информацию о стоимости всей операции приведения в соответствие активов и обязательств при условии, что она выполняется оптимальным образом.
76 4. Задача оптимизации
77 В реальной ситуации управления задан поток платежей по обязательствам Lt, а поток At составлен из промежуточных и конечных платежей по портфелю активов. Оптимальная иммунизация состоит в получении способа формирования портфеля активов, гарантирующего наилучшую оценку снизу в левой части (12). Понимая, вслед за (Nawalkha, Chambers, 1996), малость изменения форвардных ставок в смысле sup-нормы, ввиду (12), следует найти EMD-расстояние между потоками At и Lt . Чтобы схема приводила к результату (12), необходимо решить следующие задачи.
78
  1. Получить в замкнутом виде выражение для EMD-расстояния между At и Lt для последующей оптимизации по At . В противном случае две вложенные задачи численной оптимизации будут представлять техническую трудность.
  2. Одновременно (для заданных At и Lt ) находить оптимальный транспортный план ath .
  3. Доказать неулучшаемость оценки (12). В противном случае оптимизироваться будет не целевой показатель, а некоторый функционал, про который известно только, что он мажорирует целевой.
  4. Решить задачу минимизации EMD-расстояния между At и Lt , что даст искомый оптимальный портфель. Минимизация проводится по всевозможным потокам At , порождаемым различными портфелями из имеющегося набора инструментов. Одновременно будет найден оптимальный план ath , который также позволит выявить остаточные несоответствия между активами и обязательствами, т.е. то, что не может быть устранено оптимизацией. Детали таких несоответствий могут быть использованы для достижения (если потребуется) совершенного хеджа (например, через заключение соглашений о форвардной ставке (FRA)).
79 4.1. Вычисление EMD-расстояния
80 Почти готовый ответ содержится в (Валландер, 1973): для вероятностных мер P и Q на прямой
81 EMDP,Q=∫-∞∞Fx-Gxdx,  (13)
82 где Fx,Gx  — функции распределения мер P , Q .
83 Необходимо лишь конкретизировать (13) для случая дискретных мер так, чтобы результат можно было легко вычислить. В рассматриваемой задаче меры задаются величинами γt=∑hath , λh=∑tath . Рассмотрим соответствующие функции распределения: Ft=∑τ≤tγτ , Gh=∑τ≤tλτ . Функции F и G — ступенчатые (кусочно-постоянные), монотонно неубывающие, непрерывные справа, определены на 0,+∞ так, что F0=G0=0 и F+∞=G+∞=1 .
84 Предложение 1. EMDγt, λh=∑k=1N-1Ftk-Gtktk+1-tk.
85 Доказательство получается прямым применением (13) к случаю мер, сосредоточенных на конечном множестве точек tk .
86 4.2. Оптимальный транспортный план
87 Структура atht,h=1,…,N ясна из конструкции п. 4.1. Полуось времени 0,∞ разбивается на чередующиеся промежутки, где Ft<Gt и где Ft>Gt . (Случай Ft=Gt можно отнести к любому из предыдущих.) При Ft<Gt (поступления по активам запаздывают по отношению к выплатам по обязательствам) текущие выплаты нужно финансировать из будущих поступлений. При Ft>Gt  — текущие поступления используются для финансирования будущих выплат.
88 Приведем точное описание конструкции. Пусть γk=Ftk-Ftk-1  — платеж — в дисконтированном и нормированном виде — из At . В общем случае для некоторых r,q будет
89 Gtr-1≤Ftk-1<Gtr<…<Gtk<…<Gtq≤Ftk<Gtq+1.
90 При другом относительном расположении Ftk и Gtk некоторые узлы могут отсутствовать.
91 Предложение 2. В транспортном плане, реализующем EMDγt, λh , из платежа γk денежная сумма ak,r=Gtr-Ftk-1 идет на финансирование (оставшейся части) выплаты λr , ak,r+1=Gtr+1-Gtr — на финансирование выплаты λr+1 , … ak,k=Gtk-Gtk-1 взаимно погашается с (одновременной ей) выплатой λk , ... ak,q=Gtq-Gtq-1 идет на финансирование (будущей) выплаты λq , ak,q+1=Ftk-Gtq — на финансирование части (будущей) выплаты λq+1 . Остальные ak,j равны нулю.
92 Как указано выше, все денежные суммы представлены в дисконтированном и нормированном виде (рис. 1).
93

94 Рис. 1. Оптимальный транспортный план для условного примера иммунизации потока из двух выплат потоком из трех поступлений
95 4.3. Неулучшаемость оценки
96 На содержательном уровне неулучшаемость оценки (12) ясна заранее, поскольку оптимальный транспортный план — как при фиксированных At , Lt (п. 4.1, 4.2), так и при оптимизации верхнего уровня по At (см. п. 4.4), — не должен содержать встречных денежных потоков. Строго, в предложенной конструкции это можно показать следующим образом.
97 Зададим шок форвардной ставки Δi так, что при Ft<Gt (недостаточный баланс) положим Δi=δ , δ  — малое положительное число; при Ft>Gt (избыточный баланс) положим Δi=-δ ; при Ft=Gt — можно применить любой вариант из двух или положить Δi=0 . Если шок рассматривается в классе непрерывных функций, можно добиться этого, исправив Δi в малых окрестностях узлов, так что это мало изменит значения интегралов. В итоге оценка (12) будет выполняться со сколь угодно малой наперед заданной погрешностью.
98 4.4. Минимизация EMD-расстояния
99 Решение задачи оптимальной иммунизации сведено к задаче оптимизации по целевой функции minAtEMDAt,Lt. Переменной выбора будут веса в структуре активов. Для решения может быть применен какой-либо стандартный метод численной оптимизации (см. разд. 5). В результате будут получены оптимальный портфель, оптимальный поток платежей At*=argminAtEMDAt,Lt и оптимальный (верхнего уровня) транспортный план at,h* .
100 5. Апробация на реальных данных
101 В стандартном предположении о детерминированных денежных потоках портфель составляется из облигаций с минимальной вероятностью дефолта, с фиксированными купонными выплатами, без опции отзыва, не индексируемыми на темпы инфляции.
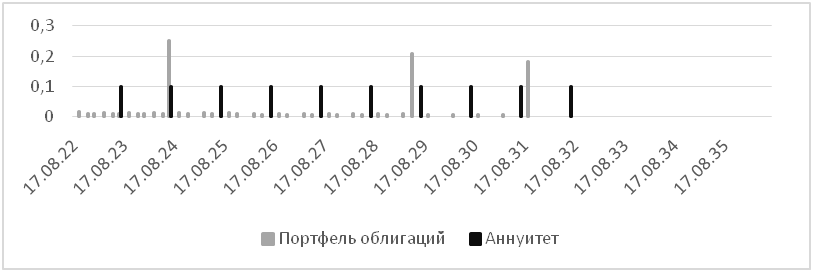
102 Для демонстрационного расчета взяты данные торгов облигаций федерального займа (ОФЗ) на Московской бирже (МБ) за 27.07.2022. Для дисконтирования использовалась спотовая кривая, рассчитанная по методике МБ, со значениями динамических параметров на ту же дату, взятыми с сайта МБ8, а в качестве набора облигаций для составления портфеля — ОФЗ ПД 26220, 26227, 26224, 26218 и 26240 со сроками погашения в 2022, 2024, 2029, 2031 и 2036 г. Данные выпуски выбраны из числа наиболее ликвидных (что проверялось в том числе малостью корректирующих поправок) и используемых в спотовой кривой. Графики купонных выплат и погашений взяты с сайта эмитента — Министерства финансов России9. В качестве потока обязательств, для примера, был взят 10-летний аннуитет с первым платежом 27.02.2023. Чтобы дополнительно продемонстрировать простоту и доступность предлагаемого метода, расчеты умышленно были выполнены в обычном табличном процессоре с модулем оптимизации (MS Excel), а не в какой-либо среде программирования. При этом время сходимости итераций градиентного спуска и точность вычислений оказались вполне удовлетворительными для практического использования. Предварительно для проверки метода в качестве пробных потоков обязательств задавались портфели из выбранных облигаций с различными соотношениями долей. Всякий раз метод успешно и точно воспроизводил эти доли в своем оптимальном иммунизированном портфеле.
8. >>>>

9. >>>>
103 В итоге решением задачи оптимизации является портфель, состоящий из ОФЗ 26227; 26224; 26218 в долях 0,28; 0,33; 0,39 соответственно. EMD-расстояние между портфелем и аннуитетом равно 0,62 по формуле (12). Для сравнения, для отдельных облигаций из списка такие расстояния равны соответственно 4,43; 3,03; 1,62; 1,75 и 3,69, т.е. мы наблюдаем очевидное улучшение. Потоки платежей по обязательствам и оптимальному иммунизированному портфелю представлены на рис. 2.
104

105 Рис. 2. Поток платежей по обязательствам и оптимальному иммунизированному портфелю
106 Заметим, что иммунизация с минимизацией EMD-расстояния не приводит к абсолютно безрисковому портфелю, это же относится к любому иммунизирующему механизму, предложенному когда-либо.
107 Современный взгляд на неопределенность на финансовых рынках таков, что хеджирование процентного риска следует понимать не как равенство конечных стоимостей ex ante и ex post в духе классической теории Редингтона, а как нахождение приемлемой верхней границы для убытков. При этом иммунизация потока множественных платежей с минимизацией меры разброса может дать даже более защищенный портфель, чем такая же иммунизация единичного платежа: активы будут структурированы равномернее, чем в залповом портфеле, структура которого является оптимальной при иммунизации единичного платежа, и как следствие, могут представлять меньший идиосинкратический риск.
108 6. Заключение
109 Финансовые посредники, управляющие портфелями чувствительных к движению процентных ставок инструментов «по обе стороны баланса» (пенсионные фонды, страховые компании, управляющие частным капиталом), регулярно сталкиваются с проблемой выравнивания денежных потоков по активам и обязательствам в условиях непрерывно меняющихся процентных ставок. Управление процентным риском является неотъемлемым компонентом их рутинной практики. В процессе своей эволюции теория иммунизации предложила ряд идейных инноваций в управлении процентными рисками, однако все они касаются только частного случая хеджирования единичного платежа. Ввиду отсутствия в рамках теории иммунизации решений для потока множественных платежей, ориентированных на практику, финансовые институты вынуждены прибегать к хеджирующим механизмам ad hoc, к примеру, — к балансировке по платежам (cash flow matching).
110 В статье предложен новый иммунизирующий механизм, универсальный в плане хеджирования потока как с единичным, так и с множественными платежами при самых общих предположениях относительно возмущения спотовой кривой. В основе данного механизма лежит сложившаяся в научной литературе (Fong, Vasicek, 1984; Nawalkha, Chambers, 1996; Balbas, Ibanez, 1998) концепция минимизации меры разброса, характеризующей чувствительность портфеля активов к возмущению спотовой кривой. В отличие от вышеперечисленных работ предложенная в настоящей работе мера разброса — EMD-расстояние — применима для оценки разброса по отношению к множественным моментам времени. Базовая конструкция — расстояние Монжа–Канторовича–Вассерштейна — успешно применяется в теории меры, теории транспортных задач, методах распознавания образов и т.д., но впервые рассматривается как инструментарий интегрированного управления портфелями активов и обязательств.
111 Для оптимизации структуры активов поставлены и решены такие задачи, как выражение EMD-расстояния в замкнутом виде, доказательство неулучшаемости оценки верхней границы убытков, нахождение оптимального транспортного плана. Действенность иммунизирующего механизма проиллюстрирована на числовой симуляции с привлечением реальных данных. Для демонстрации технической простоты метода задача оптимизации была решена в табличном процессоре MS Excel. Представляется, что, обладая как четкой теоретической трактовкой, так и высоким потенциалом практической реализуемости, модель иммунизации с минимизацией EMD-расстояния на сегодняшний день является оптимальным решением проблемы хеджирования потока множественных платежей.
112 При этом настоящая работа раскрывает потенциал дальнейшего совершенствования иммунизирующих механизмов, которого можно было бы добиться, рассмотрев снятие ряда ограничений, — таких как равенство настоящих стоимостей портфелей активов и обязательств, т.е. постановка несбалансированной транспортной задачи и запрет на короткие позиции.

Библиография

1. Бешенов С.В, Лапшин В.А. (2019). Параметрическая иммунизация процентного риска на основе моделей срочной структуры процентных ставок // Экономический журнал ВШЭ. Т. 23 (1). С. 9–31.

2. Богачев В.И., Колесников А.В. (2012). Задача Монжа–Канторовича: достижения, связи и перспективы // Успехи математических наук. Т. 67. Вып. 5 (407). С. 3–110.

3. Валландер С.С. (1973). Вычисление расстояния по Вассерштейну между распределениями вероятностей на прямой // Теория вероятностей и ее применения. Т. 18. Вып. 4. С. 824–827.

4. Balbas A., Ibanez A. (1998). When can you immunize a bond portfolio? Journal of Banking and Finance, 22, 1571–1595.

5. Balbas A., Ibanez A., Lopez S. (2002). Dispersion measures as immunization risk measures. Journal of Banking and Finance, 26 (6), 1229–1244.

6. Bayliss C., Serra M., Nieto A., Juan A. (2020). Combining a matheuristic with simulation for risk management of stochastic assets and liabilities. Risks 8 (4), 131.

7. Bierwag G. (1977). Immunization, duration, and the term structure of interest rates. Journal of Financial and Quantitative Analysis, 12 (5), 725–742.

8. Bierwag G., Fooladi I., Roberts G. (1993). Designing an immunized portfolio: Is M-squared the key? Journal of Banking and Finance, 17, 1147–1170.

9. Bierwag G., Kaufman G., Toevs A. (1983). Immunization strategies for funding multiple liabilities. Journal of Financial and Quantitative Analysis, 18 (1), 113–123.

10. Chizat L. (2018). Unbalanced optimal transport: Dynamic and Kantorovich formulations. Journal of Functional Analysis, 274 (11), 3090–3123.

11. De La Peña J.I., Iturricastillo I., Moreno R., Roman F., & Trigo E. (2021). Towards an immu-nization perfect model? International Journal of Finance & Economics, 26 (1), 1181–1196.

12. Dutta G., Rao H., Basu S., Tiwari M. (2019). Asset liability management model with decision support system for life insurance companies: Computational results. Computers & Industrial Engineering, 128, 985–98.

13. Fabozzi F.J., Fong H.G. (1985). Fixed income portfolio management. Appendix E: Derivation of risk immunization measures. Homewood Illinois: Dow Jones-Irwin.

14. Fisher L., Weil R. (1971). Coping with the risk of interest rate fluctuations: Returns to bond-holders from naïve and optimal strategies. Journal of Business, 44 (4), 408–431.

15. Fong G., Vasicek O. (1984). A risk minimizing strategy for portfolio immunization. Journal of Finance, 39 (5), 1541–1546.

16. Ford P. (1991). Some Further Investigations into Cashflow Matching. AFIR Colloquium, Rome, Italy, 539–551.

17. Ford P.E.B. (1991). Cashflow matching using modified linear programming. AFIR Colloquium, Brighton, United Kingdom, 3, 301–322.

18. Gangbo W., Li W., Osher S., Puthawala M. (2019). Unnormalized Optimal transport. Journal of Computational Physics, 399, 108940.

19. Hürlimann W. (2002). On immunization, stop-loss order and the maximum shiu measure. Insur-ance: Mathematics and Economics, 31, 315–325.

20. Ingersoll J.Jr., Skelton J., Weil W. (1978). Duration forty years later. Journal of Financial and Quantitative Analysis, 13 (4), 627–650.

21. Khang C. (1979). Bond immunization when short-term interest rates fluctuate more than long-term rates. Journal of Financial and Quantitative Analysis, 14 (5), 1085–1090.

22. Kopa M., Rusý T. (2021). A decision-dependent randomness stochastic program for asset-liability management model with a pricing decision. Annals of Operations Research, 299, 241–271.

23. Leibowitz M. (1986). The dedicated bond portfolio in pension funds – Part I: Motivations and ba-sics. Financial Analysts Journal, 42 (1), 68–75.

24. Monge G. (1781). Mémoire sur la théorie des déblais et des remblais. Paris : De l'Imprimerie Royale.

25. Montrucchio M., Peccati L. (1991). A note on shiu-fisher-weil immunization theorem. Insurance: Mathematics and Economics, 10, 125–131.

26. Nawalkha S., Chambers D. (1996). An improved immunization strategy: M-absolute. Financial Analysts Journal, 52 (5), 69–76.

27. Nawalkha S., Chambers D. (1997). The M-vector model: Derivation and testing of extensions to M-square. Journal of Portfolio Management, 23 (2), 92–98.

28. Nawalkha S., Soto G., Zhang J. (2003). Generalized M-vector models for hedging interest rate risk. Journal of Banking and Finance, 27 (8), 1581–1604.

29. Panaretos V., Zemel Y. (2019). Statistical aspects of wasserstein distances. Annual Review of Statistics and Its Application, 6, 405–431.

30. Redington F. (1952). Review of the principles of life-office valuations. Journal of the Institute of Actuaries, 78 (3), 286–340.

31. Rosenbloom E., Shiu E. (1990). The matching of assets with liabilities by goal programming. Managerial Finance, 16 (1), 23–26.

32. Shiu E. (1987). On the Fisher–Weil immunization theorem. Insurance: Mathematics and Economics, 6, 259–266.

33. Shiu E. (1990). On Redington’s theory of immunization. Insurance: Mathematics and Economics, 9, 171–175.

34. Theobald M., Yallup P. (2009). Liability-driven investment: Multiple Liabilities and the question of the number of moments. European Journal of Finance, 16 (5), 413–435.

35. Torres L., Pereira L., Amini H. (2021). A survey on optimal transport for machine learning: Theory and applications. arXiv: 2106.01963. DOI: 10.48550/arXiv.2106.01963

36. Van der Meer R., Smink M. (1993). Strategies and techniques for asset-liability management: An overview. Geneva Papers on Risk and Insurance, s and Practice, 18 (67), 144–157.

37. Vanderhoof I. (1972). The interest rate assumption and the maturity structure of the assets of a life insurance company. Transactions of Society of Actuaries, 24 (69), 157–192.

38. Weil R. (1973). Macaulay's duration: An appreciation. Journal of Business, 46 (4), 589–592.

Комментарии

Сообщения не найдены

Написать отзыв
Перевести